Three Phase AC Circuits Viva Questions
Three Phase AC Circuits Viva Questions, Viva Questions on Three Phase AC Circuits, Basic Electrical Engineering Viva Questions, Short Answer Questions on Three Phase AC Circuits, Three Phase AC Circuits Viva Questions, Engineering Viva Questions
Single Phase AC Circuits Viva Questions
Short Answer Questions
Q.1. What do you mean by a three-phase balanced load?
Ans. Any three-phase load will be balanced when the loads (impedances) connected in three phases are the same in magnitude as well as in phase.
Q.2. What is a three-phase unbalanced load?
Ans. Any three-phase load will be unbalanced if impedances in one or more phases differ from the impedance(s) of the remaining phase(s).
Q.3. Why is an unbalanced load not normally used on a 3-phase 3-wire system? Are any line/ phase voltages equal in such situations?
Ans. Normally, the unbalanced load is not employed on 3-phase, 3-wire ungrounded star-connected systems because unbalanced loading may cause different voltage drops in as well lines. Consequently, the three-phase voltages are different (or unbalanced) in magnitude as well as in-phase and it is quite possible that one phase voltage may exceed the line voltage. Such a condition is undesirable since some loads may operate inefficiently due to lowering of the voltage and the other equipment may get damaged due to over-voltage.
Q.4. Differentiate between balanced and unbalanced three-phase supply and balanced and unbalanced three-phase load.
Ans. 3-phase supply will be balanced when line-to-line voltages are equal in magnitude and displaced in phase by 120 electrical degrees with respect to each other. On the other hand, a 3-placed supply will be unbalanced when either of the three-phase voltages is unequal in magnitude or the phase angle between these phase voltages is not equal to 120°.
A 3-phase load circuit is said to be balanced when the loads (impedances) connected in the different phases are the same in magnitude as well as in phase. On the other hand, any three-phase load in which the impedances in one or more phases differ from the impedances of other phases is called the unbalanced three-phase load.
Q.5. Show by a phasor diagram that the sum of the three-phase balanced currents is zero.
Ans. For a balanced 3-phase system, all phases should have equal maximum values and should be displaced by 120 electrical degrees with respect to each other, as illustrated in the phasor diagram.
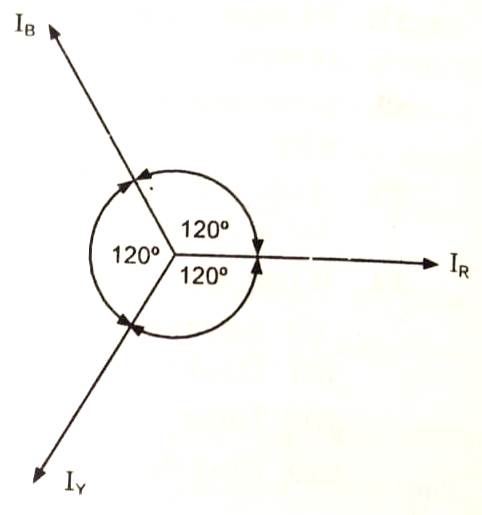
i.e. I_{R}=I_{Y}=I_{B}=I_{P}(say)
The resultant of three-phase balanced currents = I_{R}+I_{Y}+I_{B};
=I_{R}\angle 0^{o}+I_{B}\angle 120^{o}+I_{Y}\angle -120^{o} ;
=I_{R}+I_{B}\cos 120^{o}+I_{Y}\cos (-120^{o})+jI_{B}\sin 120^{o}+jI_{Y}\sin (-120^{o});
=I_{R}-\frac{1}{2}I_{B}-\frac{1}{2}I_{Y}+j\left (\frac{\sqrt{3}}{2} I_{B}-\frac{\sqrt{3}}{2}I_{Y} \right )=0;
\because I_{R}=I_{Y}=I_{B}Q.6. What do you mean by the phase sequence of three-phase supply?
Ans. The phase sequence is meant the order in which the currents or voltages in different phases attain their maximum values one after the other.
Q.7. What is phase sequence in a 3-phase system? How is the given phase sequence reversed?
Ans. The phase sequence is the order or sequence in which the currents or voltages in different phases attain their maximum values one after the other.
The given phase sequence can be reversed by interchanging any two terminals of the supply.
Q.8. Why interconnection of a 3-phase system is necessary?
Ans. The non-interlinked three-phase system will require 6 wires while the interconnected 3-phase system will require 3 or 4 wires. So non-interlinked system will be very complicated and expensive.
Q.9. Differentiate between star and delta connections.
Ans. In a star-connected system similar (either start or finish) terminals of the three phases are connected together to provide star or neutral points while in a delta-connected system start terminal of one phase is connected to the finished terminal of the second phase and the start terminal of the second phase is connected to finish terminal of the third phase and so on to provide a closed circuit in a 3-phase system.
Q.10. Discuss, why the stator windings of the alternator are generally star-connected?
Ans. In a star-connected system phase voltage is equal to \frac{1}{\sqrt{3}} times the line voltage, but in a delta-connected system phase voltage is equal to line voltage, therefore, the star-connected alternator needs less number of turns per phase and less insulation than a delta-connected alternator for the same line voltage.
The neutral point of a star-connected system can be connected to the earth, so relays and protective devices can be provided in a star-connected system for the protection of the system against ground faults and it is usually done in practice. These are the reasons that 3-phase alternators are usually star-connected.
Q.11. Why does a star-connected alternator need less number of turns per phase as compared to that required by a delta-connected one to provide the same line voltage?
Ans. In a star-connected system phase voltage is equal to \frac{1}{\sqrt{3}} times the line voltage, but in a delta-connected system phase voltage is equal to line voltage, therefore, the star-connected alternator needs less number of turns per phase than a delta-connected alternator for the same line voltage.
Q.12. Why delta-connected system cannot be employed for supplying lighting as well as power loads?
Ans. The delta-connected system cannot provide a 3-phase 4-wire system (i.e. neutral wire cannot be carried) which is essential for supplying lighting as well as power loads.
Q.13. Draw the circuit diagram for 3-phase power measurement by two wattmeters. Under what operating conditions, one of the wattmeters will show a negative reading?
Ans. The circuit diagrams for 3-phase power measurement by two wattmeters are shown in the figure below.

One of the wattmeters will show a negative reading when the power factor of the load circuit is below 0.5.
Q.14. While measuring power in a balanced three-phase circuit, one of the wattmeters keeps showing zero as the load is varied. How do you account for it?
Ans. One of the two wattmeters, in a two-wattmeter method of measuring power in a balanced 3-phase circuit, will keep showing zero as the load is varied if and only if the power factor of the load remains constant at 0.5. The reading of other wattmeters will vary with the variation in load.
Q.15. What will happen if the neutral gets disconnected in a 3-phase 4-wire unbalanced circuit?
Ans. In the case of an unbalanced 3-phase, 4-wire system when the neutral is disconnected, the loads which are connected between any two line conductors and the neutral are connected in series and potential difference across the combined load becomes equal to line voltage. The potential difference across each load is thus changed as per the rating of the load. The changes in voltages and currents are usually very large (in most cases inadmissible).
Q.16. What is meant by floating neutral in a 3-phase ac system?
Ans. If the neutral point of the load is not connected to the neutral of the generator, the phase voltages do not remain the same across each phase but vary according to the unbalancing of load and under certain conditions of loading a considerable voltage may exist between the two-star points. Such an isolated star-point is known as a floating neutral because its potential is always changing.
Q.17. Why star-connected unbalanced load is not normally used on 3-phase, 3-wire systems?
Ans. In the case of unbalanced 3-phase, 3-wire star-connected load circuits, three-phase voltages are different in magnitude and in-phase and it is quite possible that one phase voltage may exceed the line voltage. Such a condition is undesirable since some loads may operate inefficiently due to lowering of the voltage and the other equipment may get damaged due to overvoltage.