Crystal Structure of Materials Viva Questions
Crystal Structure of Materials Viva Questions, Viva Questions on Crystal Structure of Materials, Material Science Viva Questions, Engineering Viva Questions, Short Question with answer on Crystal Structure of Material, Crystal Structure of Materials Viva Questions, Crystal Structure of Materials Viva Questions, Crystal Structure of Materials Viva Questions
Material Science Engineering Viva Questions
Mechanical Properties of Materials Viva Questions
Short Questions with Answer
Q.1. What are the Structures of Atoms?
Ans. According to the modern concept, an atom is composed of the nucleus which is surrounded by electrons. The diameter of the nucleus is 10-10 m. The nucleus is further composed of neutrons and protons. It can be said that an atom consists of two main parts
- The heavy nucleus is composed of protons and neutrons, and
- The surrounding electrons.
Both are equally important for explaining the properties of materials.
Electron: An electron is the unit quantity of electrical energy with a charge of -1.602 x 10-19 C. The mass of the electron is only 1/1836 of the mass of the proton. The electrons can spin only in certain ordered energy levels or orbital shells concentric with the nucleus.
Proton: The proton is a heavy particle of mass 1.673 x 10-27 kg and it possesses unit positive charge of 1.602 x 10-19 C. The proton usually exist together with neutrons, in the nucleus of an atom.
Neutron: The neutron is little heavier, 1008 times heavier than the proton and it does not possess any electrical charge. Both protons and neutrons are called nuclei because they make the nucleus of an atom.
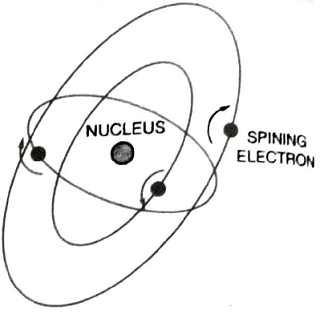
Q.2. What are Bohr’s postulates?
Ans. An electron can only revolve around the nucleus in certain fixed and discrete orbits without the emission of radiant energy. Further, only those orbits having orbital angular momentum or moment of the electrons equal to an integral multiple of h/2π are possible or permitted i.e., orbital angular momentum nh/2π, where n is an integer and h is Planck’s constant.
The electron while revolving in these orbits does not radiate any energy (or electromagnetic energy). The orbits are non-radiating paths of the electrons.
The energy is radiated by an atom only when the electron jumps from one orbit to another of lower energy.
Q.3. Describe the various deficiencies in Bohr’s theory.
Ans. Various deficiencies in Bohr’s theory can be summarized as under:
- No explanation is provided by it as to why certain spectral lines are more intense than the others resulting in a greater probability of occurrence of certain transitions between energy levels.
- It cannot explain the experimental evidence of the fine structure of spectral line suggesting additional quantum numbers instead of the planetary model which introduces only one quantum number.
- It cannot account for how individual atoms interact with one another for endowing macroscopic aggregate of matter with the physical characteristics exhibited by them.
- It cannot be easily extended to describe more complicated or many-electron atoms as it applies to any one-electron atom.
- A quantitative explanation of chemical bonding cannot be explained by it. A negative value for bond strength (bond-breaking energy) in systems like ionized hydrogen atom suggests that ions of this type cannot exist. It does exist with a bond strength of 61 kcal/mole actually.
Q.4. What do you understand by electronic configuration?
Ans. The electronic configuration of atoms of various elements is expressed in terms of quantum numbers. The electronic configuration of an atom is the distribution of its electrons in the various shells and sub-shells around the nucleus.
It follows the following rules.
- The maximum number of electrons in a shell is 2n2 where n is the principal quantum number of the shell.
- The maximum number of electrons in each sub-shell is 2(2l + 1) where l is the orbital quantum number.
- For the nth shell, there are n sub-shells with different values of orbital quantum number l.
Q.5. Write a short note on crystallography?
Ans. Crystallography is the branch of science in which the internal structure of crystals, their properties or internal symmetries possessed by crystals are studied. Before the discovery of X-rays, crystallographic science was limited to the study of the morphology of crystals i.e. external appearances and external symmetries. This was named older crystallography.
After the discovery of Laue’s diffraction of X-rays by crystals. a new idea emerges which become a science of the crystalline state. This crystallography with the aid of X-rays is known as crystallography. This helps in determining the following:
- The actual existence of shape pattern.
- Exact shape and size of crystalline solids.
- The actual periodic arrangement of atoms in space.
X-ray crystallography reveals that most of the important materials have crystalline structures.
Q.6. Define the following terms:
- Space lattice
- Unit cell
- Bravais lattice
- Coordination number
- Atomic radius
Ans.
Space lattice: It is defined as the 3-dimensional arrangement of points (Atoms, Ions or Molecules) in a space. It can also be defined as an infinite array of points in 3-D space in which each point is identically located with respect to others. These points with identical surroundings are called lattice points.
Unit cell: It is defined as the “smallest structural unit or building block that can describe the crystal structure and which when repeated in different directions gives the entire lattice. Each unit cell in space lattice is identical in shape, size and orientation with every other unit cell. Repetition of unit cell generates the entire crystal.
Bravais lattice: The fourteen distinguishable three-dimensional space lattices that can be generated by repeated translation of three non-coplanar vectors a, b and c of unit cell in three-dimensional space are known as braves lattice, named after their originator.
Coordination number: In a crystalline structure, every atom is surrounded by other atoms, which are definite. Thus, the coordination number is defined the number of nearest atoms that are directly surrounding a given atom. It may also he defined as the nearest neighbours to an atom or an ion in crystal.
Table. The coordination number of different crystal structures.
| Crystal structure | Coordination number |
| SCC | 6 |
| BCC | 8 |
| FCC | 12 |
| HCP | 12 |
Atomic radius: It may be defined as half the distance between nearest neighbours in a crystal of pure element. It is possible to calculate the atomic radius by assuming that atoms are spheres in contact in a crystal if the structure and lattice parameters are known.
The relation between atomic radius and edge length of cubic structure for the different unit cells is given below:
- For a simple cubic structure, r=\frac{a}{2}, where r is the radius of atom and a edge length of unit cell.
- For body centre cubic structure, r=\frac{a\sqrt{2}}{4},
- For face centred cubic structure, r=\frac{a\sqrt{3}}{4}
Q.7. Explain the rules for finding miller indices.
Ans. The following steps are followed for finding miller indices
- Determine the intercepts of the plane of the three co-ordinates axes, in terms of lattice constant.
- Take the reciprocal of these intercepts.
- Reduce the reciprocals into whole numbers by multiplying each with the same number (i.e. the numbers which come after taking LCM) which gives the miller indices of the concerned plane.
Q.8. Explain the term ‘Atomic Packing Factor’.
Ans. Atomic packing factor is also called relative density of packing or Atomic packing efficient (APE). It is defined as the ratio of the total volume occupied by atoms per unit cell to the total volume of the unit cell
APF=\frac{Total volume of Atoms per unit cell}{Total volume of unit cell};
APF=\frac{Effective number of atoms x Volume of one atom }{Volume of unit cell};
APF=\frac{n\times \frac{4}{3}\Pi r^{3}}{Volume of unit cell}=\frac{n\times \frac{4}{3}\Pi r^{3}}{a^{3}};
Where, r = radius of the atom, a = edge length of the unit cell
Q.9. Describe the point of imperfections with examples.
Ans. The point imperfections are also known as zero-dimensional imperfections. As the name implies, they are imperfect point-like regions in the crystal. One or two atomic diameters are the typical size of a point imperfection. A point imperfection comes out due to the absence of a matrix atom (an atom that would be present in a perfect crystal), the presence of an impurity atom or a matrix atom in the wrong place. Vacancies, interstitial, Schottky, defects, Frenkel defects, compositional defects (substitutional interstitial), and electronic defects are the examples of mos common point imperfections.
Vacancies refer to missing atoms or vacant atomic sites. Such imperfections may arise either from imperfect packing during the original crystallization or from thermal vibrations of the atoms.
In a closed-packed arrangement of atoms, if the atomic packing factor is low, an extra atom may be lodged within the crystal structure. This is known as interstitial.
The schottky defect is closely related to vacancies. A pair of the vacant sites are called Schottky.
Similarly, Frenkel’s defect is closely related to interstitialcies. Closed-packed structures have fewer interstitialcies and Frenkel defects than vacancies and Schottky defects, and additional energy is needed to force the atoms into their new positions.
Q.10. Define the term line imperfection.
Ans. If a plane of atoms only partway through a crystal, the edge of such a plane is a defect in the form of a line. Line imperfections are called dislocations. The word ‘dislocation’ is used by convention to denote only the line imperfections. The line imperfections are dimensional imperfections in the geometrical sense. Various types of dislocations are found in crystals, the most common being edge dislocation and screw dislocation.
Q.11. What do you understand by the term surface imperfections?
Ans. Surface imperfections refer to the regions of distortions that lie about a surface having a thickness of a few atomic diameters. They arise from a change in the stacking of atomic planes on or across a boundary. Surface imperfections are two-dimensional imperfections in a geometrical sense. They are of two types: external and internal.
External surface imperfections refer to the imperfections on the outer surface of the crystal. Because the outermost atoms of the crystal surface are not entirely surrounded by others, they possess higher energy than that of internal atoms, and therefore, they become distorted.
Internal surface imperfections refer to the imperfections in the inner surfaces of the crystal and include grain boundaries, tilt boundaries, twin boundaries and stacking faults.
Q.12. Describe the term thermal vibration.
Ans. It is also one of the types of crystal imperfections. No crystal is, of course, perfectly rigid. It can be deformed by finite force. Hence the atoms can be displaced from their ideal sites with a finite expenditure of energy due to thermal vibrations. The amplitude of vibration increases with the increasing temperature. When the vibration becomes strong enough, the atoms may break the bonds between them and the solid metal becomes liquid, the corresponding temperature is the melting temperature. Since the atoms interact with one another, they tend to vibrate in synchronism. The energy of a particular type of wave can be measured in units, known as phonons, the thermal energy of the entire solid is represented by a certain collection of phonons. However, the thermal vibration of atoms of a solid does not seriously disturb the perfection of the crystal.
Q.13. Define dislocation and also describe the main types of dislocations.
Ans. The dislocation can be regarded essentially as a linear disturbance of the atomic arrangement, which can move very easily on the slip plane through the crystal. The dislocation in the crystal may be produced during a slip or it may occur during the growth of crystals from a melt or from a vapour. There are two main types of dislocations:
- Edge dislocation.
- Screw dislocation.
Q.14. Define Burgers Vector and describe the Burgers circuit.
Ans. The magnitude and the direction of the displacement are defined by a vector called the Burgers vector (BV), which characterizes a dislocation line.
The Burgers vector is perpendicular to the edge dislocation line.
The direction of the Burgers vector depends on the direction of the circuit, which can be clockwise or anticlockwise. To avoid this ambiguity, a unit vector t is first assigned to denote the direction of the dislocation line. The direction vector is drawn tangential to the dislocation line at the point of interest.
Q.15. What do you understand by the dislocation theory for plastic deformation?
Ans. A dislocation is a linear lattice defect. It is responsible for nearly all aspects of the plastic deformation of metals. Basically, dislocation is of two forms:
- Edge dislocation: It is a region of lattice disturbance extending along an edge inside a crystal.
- Screw dislocation: It is a region of lattice disturbance extending in two separate planes perpendicular to each other inside a crystal.